In 1768, through careful observation and lots of computations, the Royal Society was able to compute the distance of the Earth from the Sun.  Armed with this information, and using Newtons universal law of gravitation (1687), it should be possible to understand the behavior of the planets.  There remained, however, just one problem.  How much did each of these planets weight. 

Like the computation of the Astronomical Unit where we knew the ratios of the planetary orbits but not their magnitude, computing the mass of any one planet would allow the Royal Society to compute the relative mas of all the others but how do you weigh a thing you’re standing on? That’s like being asked to weigh your own scales without using a second set of scales.

In 1687, Isaac Newton developed a mathematical description of the force of gravitation and explained three laws of motion.  Unlike the common mythology, this was not because an apple fell on his head, but rather because he carefully observed the motion of falling objects and created mathematical models to explain this behavior.  According to Newton every particle attracts every other particle in the universe with a force determined by their masses and the square of the distance between the centers of the objects. If no other significant objects are nearby (like the space between planets), you can compute this force as:

So, theoretically, if you have the mass of one of the objects and their relative distances you can figure out the mass of the other object. If the Astronomical Unit (distance of the Earth to the Sun), which we computed in 1768, is known and the mass of the Earth is known, it should be possible to calculate the mass of the Sun.  The problem is that Newton could not establish the gravitational constant because all the things he was measuring were too close to other objects (relative to their mases).  To accurately do this you needed something big (like a planet or a moon) and relatively empty spaces between those objects, or you have to work with VERY small distances.

Knowing the mass and density of the Earth would be incredibly useful for astronomers, as it would help them calculate the mass and density of other objects in the Solar System.  It was also a serious military advantage to any navy that relied on celestial observations to determine where their ships were at sea.  In 1772, the Royal Society set up the “Committee of Attraction” to solve this problem.

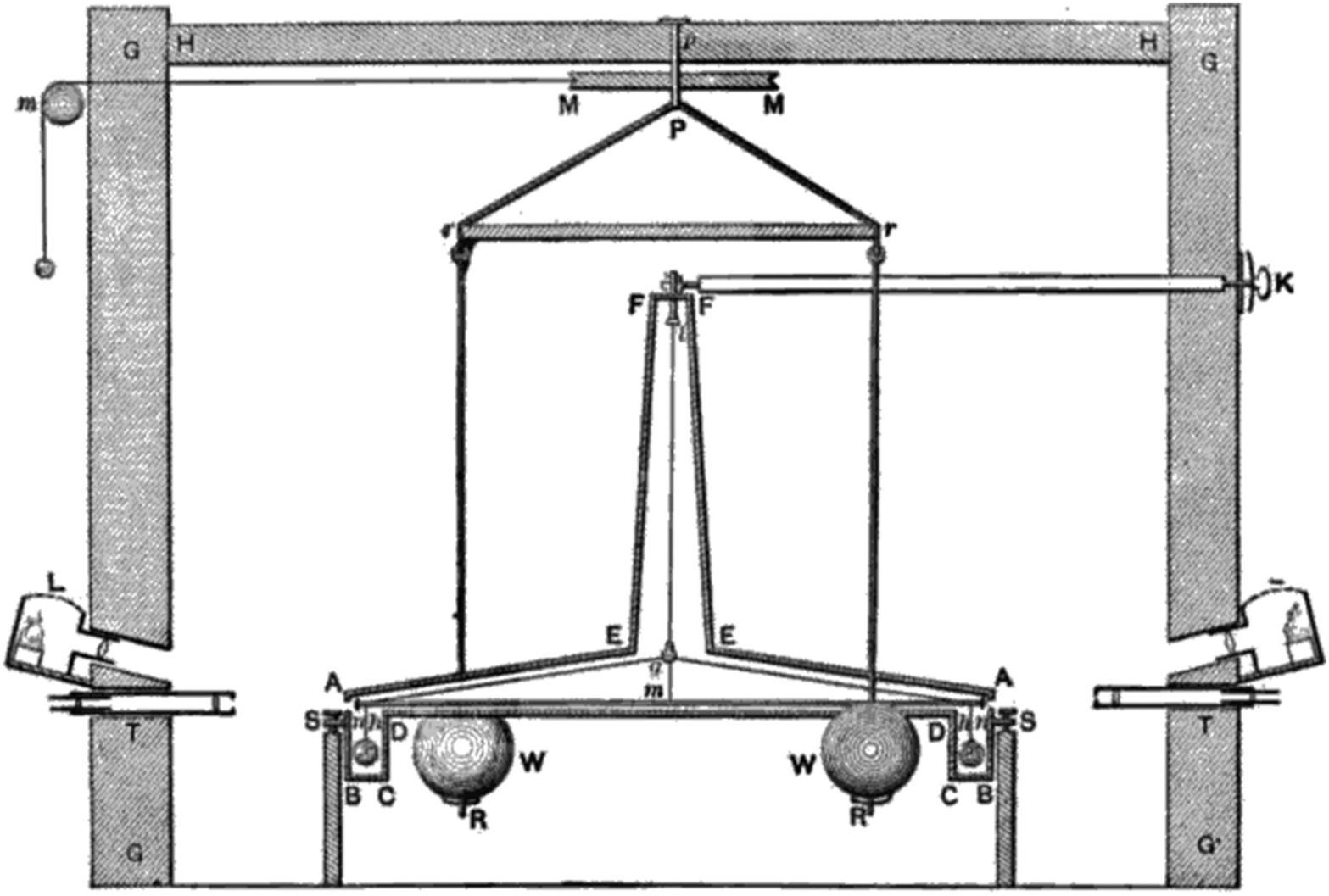
Henry Cavendish, using a relatively simple setup was able to measure the force between two metal spheres.  The system was allowed to come to complete rest (no rotational movement) then a large dense sphere was placed at a known distance from one of the smaller spheres.  Since the two spheres exert a gravitational attraction, they begin to “fall” toward each other.  By measuring the rate at which they accelerate toward each other (actually very slow) we can compute the force using Newton’s equations.  By using multiple spheres (each with a different mass), Cavendish was able to establish the gravitations constant.  It is then a simple matter of arithmetic to use the Astronomical Unit (computed in 1768) to calculate the mass of the earth as 1.37 x 10^25 pounds (5.97 x 10^24 kilograms).

---

Want to have the
Regimental Brewmeister
at your site or event?

You can hire me.

https://colonialbrewer.com/yes-you-can-hire-me-for-your-event-or-site/